1.3 宇宙のエントロピー変化
・回帰する宇宙
ボルツマンに対してポアンカレ回帰を用いた批判があったと上で述べたが、ポアンカレ回帰とは何だろうか。
それは、どんな系でも十分な時間が経てば
任意の状態に戻るという数学的な定理のことである。この「十分な時間」とはどれぐらいの長さかと言うと、1リットル程度の空気でさえ、その分子の配置が元の状態い戻るのには、次のような途方もなく長い時間になる[7,p.59]。
ポアンカレの回帰時間: T=10^(10000…000) 秒(10の「1億×1兆」乗)
この時間は「回帰時間」と呼ばれ、137億年という宇宙の年齢(10の20乗秒程度)よりはるかに長い。あなたがハァーっと吐いた程度の空気の量でさえ、その回帰時間は宇宙の年齢をはるかに超えている。したがって、「どんな状態にも戻れる」という内容は、理論的には正しいかもしれないが、現実的にはどう考えてもありえない話である。
回帰時間を想定した時間スケールでのエントロピーのゆらぎを考えると、下の図のようになるだろう[7,p.63]。確かにどの時刻から始めても、いつかはそのときのエントロピーの値に戻るだろう。しかし、微視的に完全に同じ状態に戻るのにかかる時間は非常に長い。だから、その長い時間の間に宇宙が(今のような)エントロピーの小さい状態になったとは考えづらい。
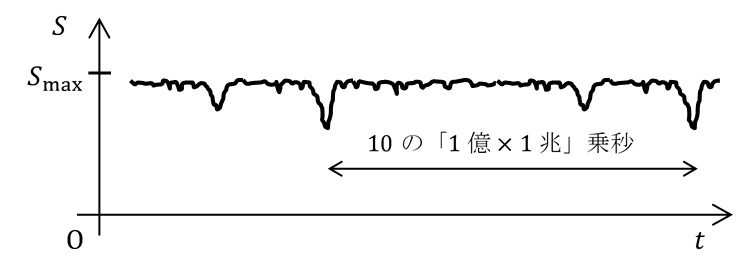
図1-9. 回帰時間スケールでのエントロピー S のゆらぎ。
確率で考えても同様である。このとてつもなく長い回帰時間を一定の時間幅で分割し、多数の時間幅の中から無作為に一つの時間幅を選んだとする。圧倒的に長い時間、ほぼエントロピー最大の状態にあるため、エントロピーの小さい時刻を選ぶ確率はとても小さい。したがって、私たち人類がエントロピーの小さい宇宙にいるのはとても不自然なことになる。
ところが、宇宙の大きさを考慮すると話が変わる。宇宙は非常に大きいため、観測限界の大きさを単位として宇宙を分割したとしても、非常に大きな数に分割できる。これに先ほどの確率を適用すると、エントロピーが小さい領域は非常に少ないが、宇宙のどこかに必ずあると考えられるようになる。
こうしてボルツマンは次のように考えるに至った[1,pp.49-50]。この世界の低エントロピー状態はきわめて例外的だが、それはまた、十分な時間を与えられれば(宇宙のどこかの領域で)当然起こるものでもある。したがって、ある意味で例外的なのは、私たちの世界のような領域(それ自体は十分に大きな宇宙のなかでは当然あって良いものだが)が「存在する」ことではなく、私たちがたまたまそうした領域にいることである。
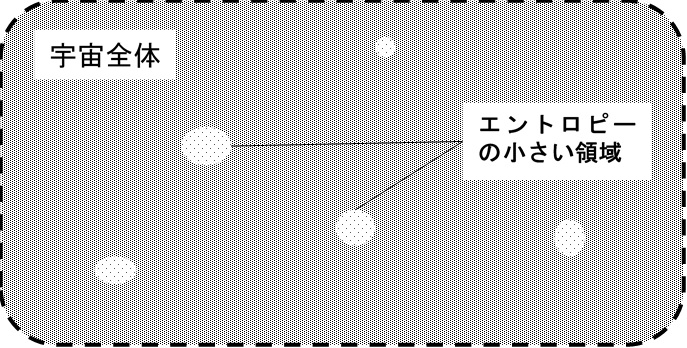
図1-10. 私たちはたまたま、宇宙の中でエントロピーの小さい領域にいるだけかもしれない。
ボルツマンはこうも言っている。生命そのものが低エントロピー状態に依存していると考えるのは当然なことである。その依存のしかたは、「低エントロピー状態にない宇宙領域に知性は存在しえない」と言っても良いほどである。プライスによれば、これは「人間原理」と呼ばれる論法の走りである。人間原理とは、「なぜこうなったか」と問う人に対して「こういう理由でこうなった」と答えるのではなく、「そうでなければ人類が存在しなかったからだ」と答え、それを説明とする方法である。つまり、そうなったのは偶然かもしれないが、人類が存在するためには必然(十分条件)だったという意味である。
ボルツマンの説明には、もう一つ気になる点がある。それは、下の図のようにエントロピーの小さい状態が出発点として選ばれたとしても、エントロピーが増大する向きは過去(A)と未来(B)の二通りあるということである。つまり、その時刻から未来に向かってエントロピーが増大する場合もあるし、過去に向かって増大する場合もあるだろう。
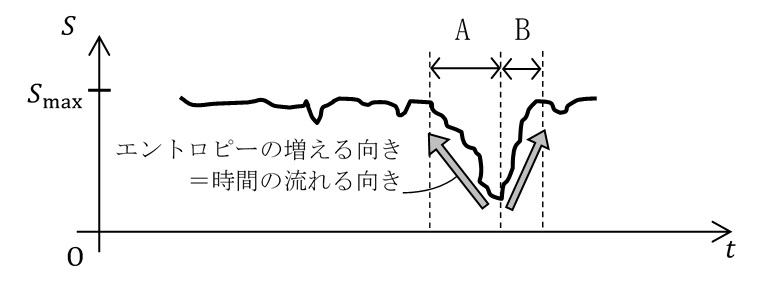
図1-11. 時間帯AとBでは逆向きに時間が流れると考える。エントロピーの増加が時間の向きを決める。
この問題に対してボルツマンはこう答える[1,p.51]。私たちのようにエントロピーゆらぎの坂の上で暮らしている生物は、エントロピーが増大する方向を未来と受け止めざるをえない。なぜなら生物学的な過程が、そうなるような形でエントロピーの傾きに依存しているからである。したがって、上図のようにエントロピーが未来に向けて増大する時間帯Aと過去に向けて増大する時間帯Bがあったら、時間帯Aでは時間は未来に向かって流れ、時間帯Bでは過去に向かって流れると生物は感じるはずである。
この説明であれば、時間の向きを決めているのはエントロピーの変化であり、それが増大する向きが時間の向きとして定義されることになる。そのため、どの時刻を選んだとしても問題は生じない。
・現代物理学における膨張宇宙とエントロピー増大
ボルツマンによれば、宇宙全体としてエントロピーは増加も減少もしていないということだったが、多くの物理学者が信じているもう一つ別の見方がある。それは、宇宙のエントロピーは初期に非常に小さい状態から始まり、その後、徐々に増えてきたという考え方である。現代の物理学者の多くもそのように考えているはずだ。
この考え方であれば、物理法則が時間対称であっても、現実の世界が非対称であることを説明できる。世界が時間について非対称である理由は、宇宙の初期条件と終条件が同じでない(非対称だ)からである。つまり、非対称性の原因は境界条件にあるというわけだ。
これによりボルツマンに浴びせられたいくつもの批判は回避できる。ロシュミットの可逆性反論は物理法則の可逆性(対称性)に基づく批判だったが、もはや非対称性の原因を物理法則に求めていないのだから問題が消える。また、ツェルメロのポアンカレ回帰の問題は、有限な宇宙の年齢と大きすぎる回帰時間から自然と解決する。つまり、初期条件でエントロピーが十分小さければ、現在の宇宙の年齢をもってしてもエントロピーが再び同じくらい小さくなるほどの時間に経過しないということだ。
ただし、非対称性の原因を初期条件に求めた場合、次の疑問が生じる。
「なぜ宇宙の初期はそんなにエントロピーの小さな状態だったのか?」
初期宇宙の低エントロピー状態は偶然の産物か。それとも何か明確な理由があったのか。現代物理学においても、この問いに対する答えはまだ統一されていない。ここで、(昔のものから最近のものまで含めて)いくつか典型的な答えを紹介しよう。
【答え1】「宇宙初期の低エントロピー状態は偶然の産物」
第一の答えは「偶然の産物である」というものである。たまたま低かったのだ。ただし、その偶然が生じる可能性は極めて小さい。R.ペンローズはその確率を P=1??10?^(?10?^123 ) と見積もっている[27]。この答えは人間原理と組み合されることが多い。先ほど述べたように、「そういう宇宙が誕生したのは偶然だが、その偶然が起きなければ人間は誕生しなかったのだから、それは必然だ」というわけだ。また、「初期状態は宇宙の境界条件の問題だから、それは物理法則では説明できない」とする考え方もある。答えの必要性自体を否定してしまうのだ。
【答え2】「理論的な必然である」
第二の答えは「それは必然であり、宇宙モデルによって理論的に説明できる」というものである。
1960年代に提案され、一時広く支持されたモデルとしてT.ゴールド、H.ボンディ、F.ホイルの定常宇宙論がある[7,p.109,; 28,p.193]。このモデルでは、宇宙の膨張とともに物質が一様に生み出され、それにより負のエントロピーが発生し、宇宙が平衡状態へ向かうのを防ぐと考える。定常宇宙論は当時、かなり支持されたが、宇宙マイクロ波背景放射の観測と合わなかったため現在は支持を失った[7,p.126]。ただ、宇宙の膨張とエントロピー増大の関係に着眼した点は重要な貢献だったと言える。
1980年代にはインフレーション宇宙のモデルが提案された。インフレーション宇宙とは、宇宙のごく初期に指数関数的な膨張が起きたとするモデルである。これにより宇宙の地平線問題や平坦性問題などが解決する。このインフレーションによって宇宙初期の低エントロピー状態を説明できると考える物理学者もいる。例えば、デイヴィス[29]やホーキングはインフレーションによって説明できるとしている。
量子重力理論などさらに別の宇宙モデルによって説明しようとする物理学者もいる。量子重力理論は重力理論と量子論を融合した理論である。それが完成すれば影響は大きいが、観測や実験による決定的な証拠を見出せていないため、複数の理論が乱立している。有名な理論としては、超弦理論やループ量子重力理論がある。そして、それらに基づいてサイクリック宇宙モデルやマルチバース・モデルなどいろいろな宇宙モデルが提案されている。サイクリック宇宙モデルでは「宇宙の再生」が起こり、マルチバース・モデルでは「赤ちゃん宇宙の誕生」などが起こるため、宇宙初期の低エントロピー状態が説明できるとする考え方もあるが、詳細は省略する。(詳細は文献[30-32]を参照してほしい。)
【答え3】「わからない」(現在のデータだけでは不明)
第三の答えは、現在までに得られたデータではわからないというものである。次の科学者たち(H.リーヴズ、S.M.キャロル、B.グリーン)はそう考えているようである[33-35]。
「私は以下のページで、物質がすでに宇宙の最初期から、複雑さへの上昇を開始し継続するのに必要なすべての情報を持っていたことを示そうと思う。だが、「なぜ物質はそうした情報を含んでいたのか」と問われれば、科学はいまだその答えを与えてはくれないのである。」
(H.リーヴズ(宇田川博訳)、「宇宙・エントロピー・組織化」、国文社(1992), p.95)
「エントロピーが小さい状態はとても「まれ」であることを考えると、宇宙初期にエントロピーが小さかったのはとても不自然に思える。… 重力が宇宙の進化に重要な役割を果たしてきたことは明らかだ。だが、残念ながら、私たちは重力を考慮したエントロピーを完全には理解できていない。」
(S.M.キャロル(前田恵一、小林努訳)、「『時間の矢』の宇宙論的起源」、日経サイエンス、2008年9月号, p.36)
「ビッグバンの時点でのエントロピーは今日よりずっと低かったはずだ。これはどう考えたら良いのだろう。… 宇宙の起源に関する完全な理論が得られていないため、科学はこの問いに答えることができない。」
B.グリーン(青木薫訳)、「時間の終わりまで」、講談社(2021), pp.99-100)
・時間の向きは今も未解決
上記の3種類の答えのうち、「答え1」は原因を偶然に求め、「答え3」はわからないと言っている。よって、理由を述べているのは「答え2」だけである。そして、「答え2」の中で量子重力理論などを用いる答えは未完成だから、唯一、ちゃんと答えているのはインフレーション宇宙モデルだけに見える。この説を支持するデイヴィスは「宇宙は…きわめてはっきりと特定される状態からではなく、任意の状態から始まった」[7,p.133]と言っている。つまり、宇宙がどんな状態で誕生してもインフレーションがあれば低エントロピー状態を用意できると考えるわけだ。
しかし、インフレーションでは説明できないとする物理学者も多い。グリーンはこの点について次のように明言している[35]。
「斥力的重力を生じさせてビッグバンをスタートさせるためには、…(中略)… 場の値が均一になった小領域が必要だ。…(中略)… しかし、激しく変動する混沌とした場の中に均一な領域を見つけるのは、大鍋いっぱいに煮えたぎるお湯の表面に、突如として平坦な領域が生じたのを見つけるようなものだ。そんなものが見つかったことは、かつて一度もない。見つからない理由は、…(中略)… 起こる確率がとてつもなく低いからだ。」
(B.グリーン(青木薫訳)、「時間の終わりまで」、講談社(2021), pp.98-100)
キャロルも以下のように、グリーンと同様の指摘をしている[34]。
「インフレーションが始まる必要条件は極めて特殊であり、それゆえエントロピーがとても小さい状態だ。もし宇宙の状態をランダムに選ぶことになったら、インフレーションが始まるのに適した条件を引き当てるなんてことは、とてもじゃないがあり得ないだろう。インフレーション自体は、なぜ初期の宇宙がエントロピーの小さな状態だったかを説明しない。初めからそれを仮定しているのだ。」
(S.M.キャロル(前田恵一、小林努訳)、「『時間の矢』の宇宙論的起源」、日経サイエンス、2008年9月号, p.29)
これらと違う考え方をしているのが、先に引用したロベッリである。彼は著書「時間は存在しない」(2019)で次のように述べている[36]。
「過去と未来の違いはすべて、かつてこの世界のエントロピーが低かったという事実に起因しているらしい。ではなぜ、過去にはエントロピーが低かったか。(p.142)
宇宙のエントロピーが最初は低く、そのため時間の矢が存在するのは、おそらく宇宙そのものに原因があってのことではなく、わたしたちのほうに原因があるのだろう。(p.146)
この宇宙のような広大な宇宙に「特別な」部分集合があったとしても、まったく驚くにはあたらない。「誰かが」くじに当たったからといって、驚くようなことではないのだ。なぜなら、毎週誰かがくじに当たっているのだから。過去に宇宙全体が信じられないくらい「特別」な配置だったと考えるのは不自然だが、宇宙に「特別な」部分があったと考えるのはまったく不自然ではない。
この意味で宇宙のある部分集合が特別だとすると、その部分集合に関しては、過去の宇宙のエントロピーは低く、熱力学の第二法則(エントロピー増大の法則)が保たれる。そしてそこには記憶が存在し、痕跡が残り−生命や思考や進化が生じ得る。」(p.148)
(C. ロベッリ(冨永星訳),「時間は存在しない」,NHK出版(2019), pp.142-148)
このロベッリの考え方はボルツマンの考え方とほとんど同じだと言って良いだろう。つまり、人間原理の復活だ。なぜか知らないが広大な宇宙の
どこかにたまたまエントロピーの非常に低い特殊な場所ができ、そこだけエントロピーが増大している。そういう場所だからこそ生命や知性が誕生できるという考え方である。しかし、この考え方には納得しがたいところがある。それは、グリーンが言った通り、「大鍋いっぱいに煮えたぎるお湯の表面に、突如として平坦な領域が生じたのを見つけるようなもの」で「起こる確率がとてつもなく低いから」である。読者の皆さんはどう考えるだろうか。
ここまでいろいろな考え方を紹介してきたが、結局、ボルツマンを追いつめた
時間の向きの問題はまだ解決していないと言えるだろう。この問題は近年、暗黒物質や暗黒エネルギーも絡む難しい問題となっている。しかし、だからこそ魅力的な課題だと考えることもできる。今後の進展が非常に楽しみである。
========================
【コラム】ボルツマンからアインシュタインへ(2):光のエントロピー
ボルツマンは1884年に気体分子運動論を「熱輻射」に適用することを考えた。
「輻射」とは光のことで、「熱輻射」とはある温度を持つ物体と平衡状態にある光のことである。
(以下、安孫子の説明[37]に基づいて解説する。)
ボルツマンは、空洞を両面鏡で区切って急激に一方に動かす場合を考え[17]、
そこにマクスウェルの輻射圧の理論を適用して、
黒体輻射のエネルギーの式 U ∝ VT^4 を得た(T は温度、V は空洞体積)。
これは現在、シュテファン・ボルツマンの法則と呼ばれている。
ヴィーンは熱源(空洞壁)から黒体輻射への熱移動を想定し、dS=dU/T+p dV/T を
積分して S ∝ VT^3 を得た(S は光のエントロピー)。
これらの研究はプランクやアインシュタインの光量子論につながった。
アインシュタインはヴィーンの公式を用いて、空洞の体積が V_0→V と変化するとき、
輻射のエントロピーが S = k log(V/V_0 )^(E/(hν)) だけ変化することを示した
(ν は光の振動数、h はプランク定数)。ボルツマンの原理 S = k log P+定数 と比較すれば、
輻射のエネルギー E が体積 V_0 にあり、Vの中だけに集中する確率がP=(V/V_0 )^(E/(hν))
で与えられることがわかる。これは N 個の理想気体における確率 P=(V/V_0 )^N と合っており、
輻射のふるまいがエネルギー hν をもつ分子のふるまいと同じであることを意味する。
これが光量子論の骨子である。
ボルツマンが新時代の扉を叩き、プランクやアインシュタインがその扉を開けた。
筆者はそういう事実を知るたびに、ボルツマンがもう少し生きていたらなあと思わずにいられない。
========================


