1.2 なぜ時間は過去に進まないか
・エントロピー増大の法則
物理法則の中に「時間の流れ」がないと述べたが、時間の観念にはさらに重要な問題がある。それは、
「時間の向き」(過去と未来の非対称性)の問題である。なぜ時間には「過去から未来へ」という向きがあるのだろうか。なぜ時間は「未来から過去へ」しか進まないのだろうか。その答えを物理法則に求めても、ほとんどの物理法則は答えを示さない。基本的に物理法則は過去と未来を区別せず、時間を「過去から未来」に見ても、「未来から過去」に見ても、どちらでも成り立つ。つまり、時間対称なのである。
例えば、ボールを真上に投げ上げた場合を考えてみよう。投げたボールは最高点に達した後、落ちてくる。これをビデオに撮って逆回しで再生してもおかしく見えない。やはりボールは上がった後、落ちてくるだけである。つまり、順向きも逆向きも同じように見えるので、時間を逆回しにしても同じ物理法則が成り立っていることがわかる。
ところが、床にボールを落とした場合は違ってくる。この場合、ボールは床でバウンドしながら、徐々に低くなっていく。これをビデオに撮って逆回し再生すると、床で静止していたボールが急に跳ねはじめ、バウンドしながら徐々に高くなっていくことになる。このような現象は実際には起きない(図2-4)。つまり、この現象の時間逆回しは自然には起きないのだ。
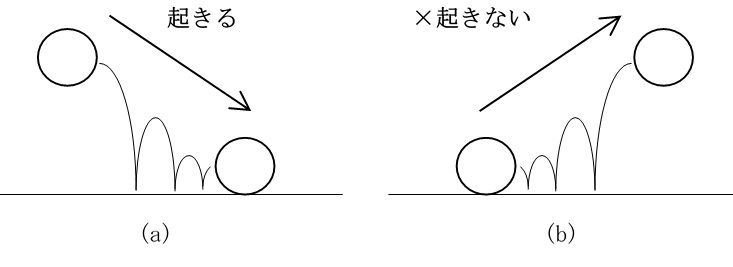
図1-4. (a)バウンドは徐々に小さくなるが、(b)自然に大きくはならない。
こうした時間の非対称性(過去と未来の違い)をニュートン力学で説明することはできない。なぜならニュートン力学の基本法則である運動方程式は、過去と未来について対称だからである。運動方程式の時間を反転させても、方程式の形は変わらない。よって、過去から未来に向けて起きる現象は、未来から過去にも起きる。それでは、なぜボールのバウンドは徐々に小さくなるだけで、徐々に大きくなることはないのだろうか。
ボールのバウンドのように未来向きだけで起きる現象のことを、物理学では「不可逆現象」と言う。「不可逆」とは「逆向きの変化が不可能」という意味である。逆向きの変化が可能な場合、「可逆」と言う。現象をビデオに撮って逆回し(時間反転)で見たとき、おかしく見える現象が「不可逆現象」で、おかしく見えない現象が「可逆現象」である。
自然現象を調べると、不可逆な現象がいくつもあることに気づく。P.C.W.デイヴィスは「時間の物理学」(1974)[7]の中で不可逆現象を次の4種類に分類した。
1)エントロピー増大の法則 ガラスのコップが床に落ちて砕け散る現象や、床を転がっていたボールが摩擦のせいで徐々に止まる現象などがこれに当たる。上で述べた、ボールのバウンドの例もここに入る。
2)宇宙の膨張 宇宙は誕生から現在まで常に膨張してきたので、現在から過去と未来を見渡せば、宇宙の時間は非対称である。
3)電磁波放射 アンテナから電磁波が放出されるときはアンテナから外向きに電磁波が広がっていきますが、時間反転した現象、つまり、電磁波が一点に集まってくるような現象は自然には起きない。
4)K中間子の崩壊過程 K中間子の崩壊は時間反転で同じにならないことが知られている。つまり、時間非対称な素粒子現象である。
私たちが目にする不可逆現象のほとんどはエントロピー増大に起因するもの(第一のグループ)である。例えば、熱いお湯と冷たい水を混ぜるとぬるま湯になるが、これもエントロピー増大によるもので逆向きの現象は起きない。また、ボールのバウンドの例もエントロピー増大による。バウンドの際に運動のエネルギーが熱に変わり、エントロピーが増大する。逆に、熱が運動のエネルギーに変わることはないので、逆の過程が起きない。
・エントロピーとは何か
エントロピーの増大が多くの不可逆現象を生み出すわけだが、そもそもエントロピーとは何だろうか。エントロピーは19世紀の熱力学(熱の物理の研究)で見つかった概念である。それは次のように定義される。
エントロピー = 熱 ÷ 温度
現実の世界ではこの量が増え続けている。これをエントロピー増大の法則という。なぜエントロピーは時間とともに増え続けるのだろうか。この問題は非常に難しく、物理学者の間で今も議論が続いている。
J.C.マクスウェルとL.ボルツマンはエントロピー増大の法則をミクロな視点から説明しようとした[8,9]。19世紀後半のことである。彼らの理論は「気体分子運動論」と呼ばれている。それによって明らかにされたことの一つは、下の図(a)のように分子の配置が無秩序で均一な状態ほどエントロピーが大きく、右図(b)のように秩序があって不均一な状態ほどエントロピーが小さいということである。つまり、エントロピーは分子の分布における「無秩序さ」や「均一性」を表している。
エントロピー = 「無秩序さ」や「均一さ」を表す量
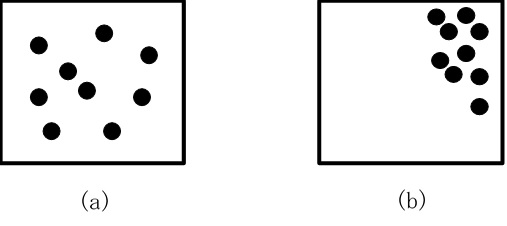
図1-5. 左(a)の方が右(b)よりエントロピー(無秩序さ)が大きい。
気体分子運動論によれば、エントロピーは分子の確率の対数の平均で表される。
エントロピー = 確率の対数の平均
「対数の平均」という言葉は聞きなれないと思うが、要するに、エントロピーが大きいほど、その状態の実現確率が高いということである。したがって、エントロピー増大の法則は、より実現しやすい無秩序な状態へと徐々に変化していくことを表している。こうしてなぜエントロピー増大の法則がなぜ成り立つのかをミクロな分子の視点から理解できた。繰り返すが、エントロピーが増加するのは、エントロピーの大きいデタラメな状態の方が、より実現確率が高いからである。これは、かなりわかりやすい説明だと思われる。
・マクスウェルの悪魔
エントロピー増大の法則はボルツマンが出した論文によって一見、うまく説明できたかのように見えた。しかし、その説明では納得できない物理学者はいまだに多い。なぜ納得できないのかと言えば、基本的に物理法則は時間対称であり、時間に非対称なエントロピー増大の法則と合わないからだ。ボルツマンの説明では、その矛盾をきちんと解消しきれていないように見える。
もう少し詳しく説明しよう。マスクウェルやボルツマンの気体分子運動論は、多数の分子の運動にニュートン力学を適用した理論である。つまり、その基礎にはニュートン力学が組み込まれている。そして、ニュートン力学は時間対称な形をしている。したがって、時間対称なニュートン力学から、時間非対称なエントロピー増大の法則が出てくることはありえないのだ。
この問題の本質には、世界が本当に時間非対称かどうかという問題が関わっている。エントロピー増大の法則が真の法則(正しい)とすれば、時間は本当に非対称であることになる。逆に、それが誤っているのであれば、時間は本当のところ対称で過去と未来に違いはないということだ。
読者は驚くかもしれないが、マクスウェル自身はエントロピー増大の法則が原理的には破れると考えていた。それは彼が友人に書いた手紙からわかる。その手紙の概要は次の通りだ[10,p.36]。(太字強調は筆者(白井)による。)
「今、容器の中に気体が閉じ込められているとしよう。容器の真ん中に壁があり、
容器は二つの部屋に分けられている。壁には穴が開いていて、
穴を開閉できる扉も付いている。この扉を開け閉めするのに物理的な仕事は必要なく、
エネルギーもいらない。『ここで、ある有限の生き物を想像してほしい』とマクスウェルは言う。
その生き物はさっと見ただけですべての分子の速度がわかるが、
壁に開いた穴を開けたり閉じたりする以外には何もしない。
この生き物は、分子の速さを見ながら穴を開けたり閉めたりすることで、
右の部屋に高速の分子ばかりを集め、左の部屋に低速の分子ばかりを集めることができる。
したがって、この作業を続けると、右の部屋はより高温になり、左の部屋はより低温になっていく。
つまり、温度差が広がり、二つの部屋の気体全体のエントロピーが減少する。
したがって、この生き物は物理的な仕事をまったくせずにエントロピーを減少させることができる。
つまり、うまくやればエントロピー増大の法則を破ることができてしまう。」
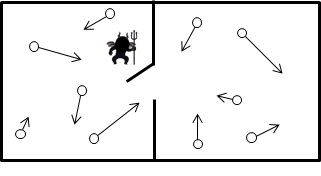
図1-6. マクスウェルの悪魔は穴の開閉でエントロピーを減少させる。
この架空の生き物の例を用いてマクスウェルが言いたかったことは、エントロピー増大の法則が
原理的には破ることが可能だということだろう。マクスウェルは次のように述べている[10]。
「… もしそのような物質の部分の一つ一つを別個に扱えるような道具を使えれば、… 温度にむらのない一つの系から、
異なる温度が複数の系 … を復元できる。ただ、我々にはそれが不可能だ。我々はそこまで利口でないから。」
(T. ノーレットランダーシュ(柴田裕之訳),「ユーザーイリュージョン」,紀伊國屋書店(2002), p.38)
このようにマクスウェルは、エントロピー増大の法則を破ることは(人間の有限な能力のため現実には無理だが)、原理的には可能だと述べた。マクスウェルのこの指摘は、現代まで続く大きな問題を物理学の世界に残すことになった。現在、この架空の「生き物」は「マクスウェルの悪魔」と呼ばれ、19世紀から現代まで議論が続いている。マクスウェルの悪魔は存在可能か(エントロピーは減少させられるか)、それとも不可能か。
現代まで続く「マクスウェルの悪魔」の議論には、大きな二つの流れがある。一つは、エントロピー増大(時間の非対称性)を理論的に導出しようとする研究である。ボルツマンがその先鞭をつけ、ポアンカレ回帰によるツェルメロの批判などを経て、宇宙のエントロピーの議論へと発展していった。
もう一つの流れは、エントロピー増大の法則を破ることが原理的に不可能であることを証明する研究である。マクスウェルの悪魔がどのような物理的理由で存在できないのかを示す研究と言って良い。こちらはL.シラードによって議論され[12]、L.ブリルアン[13,14]、R.ランダウア[15]、C.ベネット[16]、W.ズーレク[17]、そして沙川貴大[18] と現代も盛んに研究が行われている。こちらは後ほど詳しく紹介する。
・ボルツマンからアインシュタインへ
一つ目の議論の流れから見ていこう。エントロピー増大の法則を理論的に導出したとボルツマンが論文で主張したのは、マクスウェルが著書「熱の理論」[19] で「マクスウェルの悪魔」を紹介した翌年(1872年)のことだった。普通に考えれば、時間対称な理論から時間非対称な法則を導出できるはずがない。それでは、なぜボルツマンが導出できたかというと、彼が気体分子運動論の確率論的な側面に着目したからである。
ボルツマンが用いたのは分子の速さに対する確率分布で、これを用いてH関数と呼ばれる新しい関数を定義した。そして、確率の入ったその量(H関数)の時間変化を調べ、それがつねに減少することを証明した。(その証明は現在、「H定理」と呼ばれている。)H関数はエントロピーにマイナスをつけた量(負のエントロピー)であるため、H関数が常に減少することは、エントロピーが常に増えることを意味する。したがって、ボルツマンによるH関数減少の法則の証明はエントロピー増大の法則の証明に等しかった。
しかし、この主張は数々の批判を浴びた。まず、ボルツマンと同じ大学のJ.J.ロシュミットが、原子の速度をすべて逆向きにすれば、逆向きに時間をたどることになるので、過去に向かってエントロピーが増大する(未来に向かって減少する)はずだと主張した。(可逆性反論、1876)。
さらに、E.F.ツェルメロは、ボルツマンのH定理がポアンカレ回帰定理と矛盾することを指摘した(1896)。ポアンカレ回帰定理とは、「一つの孤立系では、どんな状態にも任意の近さまで有限な時間で戻ることができる」と言う定理である[7,p.59]。簡単に言えば、気体の状態は十分に時間がたてば最初と同じ状態に必ず戻るという数学的な定理である。したがって、エントロピーの低い状態から出発し、徐々にエントロピーの高い状態へ移ったとしても、いつかまたエントロピーの低い状態に戻ってしまう。これは、エントロピーが常に増え続けるという主張と矛盾している。
ボルツマンへの批判はこれだけにとどまらなかった。気体分子運動論の根底にある原子説への批判も続いた。批判者にはP.デュエム、H.ポアンカレ、W.オストヴァルトなど著名な物理学者や数学者がおり[10,p.12]、特にE.マッハからの批判は激しかった。マッハは「根拠のない原子説を信じるのではなく、エネルギーの概念を用いるべきだ」と主張し、エネルギー説を展開した。ボルツマンは最後まで原子説を擁護したが、徐々に疲れ果て、ついに次のように言うようになった。「私は、… これらの理論のために全力を挙げて戦う人間で唯一残っている者と言っていいかもしれない。」[11,p.35] その後も論争は続き、ついにボルツマンは心を病んで、自ら命を絶ってしまった。1906年のことだった。
現在から見ると、当時(1900年前後)は物理学の転換期だったように見える。1900年にM.プランクが量子仮説を提唱し、新しい物理学(量子力学)が生まれつつあった。1905年には当時無名だったA.アインシュタインが4つの論文を発表した。光電効果の理論、ブラウン運動の理論、特殊相対性理論、質量とエネルギーの等価性に関する理論である。その偉業により現在、その年は「奇跡の年」と呼ばれている。
アインシュタインの登場(1905)とボルツマンの死(1906)のタイミングを考えると残念でならない。アインシュタインの4つの論文のうち一つ(第二論文)はブラウン運動の理論だ。それは分子の存在を仮定した理論で、ボルツマンの原子説を裏付ける内容だった。奇跡の年の5年前(1900年)、アインシュタインはガールフレンドに宛てた手紙で次のように述べている[10]。
「ボルツマンは素晴らしい解説者だ。彼の理論の原理が正しいことを、ぼくは確信している。」
(P. コヴニー,R. ハイフィールド(野本陽代訳),「時間の矢、生命の矢」,草思社t(1995), p.210)
図1-7. ボルツマンの墓をよく見ると「S=k log W」と記されている。
ボルツマンがもう少し長生きしていれば、原子の存在を誰も疑わない時代が来ただろう。また、アインシュタインとは気が合ったに違いない。ボルツマンの墓には彼の偉業を記念してエントロピーを表す式「S=k log W」が記されている。
今の時代に分子や原子の存在を疑う物理学者はまずいないだろう。たった百年でそれほど状況が変わった。今では走査型トンネル顕微鏡を使えば、金属表面上に並んだ原子の配列を写真に撮ることができる。下の図は走査型トンネル顕微鏡の画像を模写したものだが、このように画像の中に1個1個の原子が(ぼやけながらも)区別できるほど見えていて、その並び方もわかる。そのような画像を見れば、誰も原子や分子の存在を疑わなくなるだろう。しかし、ボルツマンの時代には原子や分子の仮説に反論する人たちが大勢いたのである。

図1-8. 走査型トンネル顕微鏡画像の模写。個々の原子の位置がわかる。
・マクスウェルの悪魔が支払うコスト
「マクスウェルの悪魔」の話に戻ろう。「マクスウェルの悪魔」に関する研究の第二の流れは、エントロピー増大の法則が破れないこと(マクスウェルの悪魔が不可能なこと)を示す研究である。マクスウェルの死後、その流れがどうなっていったのかを紹介したい。
マクスウェルやボルツマンが亡くなった後、1929年にシラードはある論文の中でマクスウェルの悪魔が
知識を得るのにかかるコストについて考察した[12]。彼は、容器に1個だけ分子を入れた状態を考えた。
悪魔は二つの部屋のどちらに分子があるかを観測してその「知識」を得ることができるのだが、
ただで「知識」が得られるわけではない。悪魔が観測する際にどうしても分子と相互作用しなければならない。
その際、どうしてもエントロピーが増えてしまう。よって、気体だけでなく
観測者(悪魔)まで含めた全体のエントロピーは増大するはずだ。
この回答は、観測者(悪魔)を考察の対象となる物理系の一部と見なすべき
という新しい発想を生み出した。
その後、1956年にブリルアンが、悪魔が観測の際に支払うコストについてさまざまな場合を計算し、
どの場合にもエントロピーが増大することを示した[13,14]。1961年にはランダウアが、
コストは知識を得るときにかかるのではなく、
そこで得た情報を捨てるときにかかるという新しい考え方を示した[15]。
さらに1982年にベネットは、観測するのにコストがかからない例(ブリルアンに対する反例)について考察し、
次のように結論した。マクスウェルの悪魔がエントロピー増大の法則を破るためには分子を観測しなければならないが、
そのためには以前の観測結果を忘れなければならない。結果を忘れることは情報を捨てることであり、
そこで熱力学的なコストがかかる。
ところが、沙川は2008年に熱力学の第2法則をより一般的な形に書き換えて、
情報を捨てるのにコストがかからないという斬新な考えを提示した[20,21] 。
彼は次のように結論している。(太字強調は筆者(白井)による。)
「歴史的には、シラードがすでに、メモリの自由度を考えることの重要性を認識していた。
その後ブリルアンが『測定のプロセスで余分なエントロピー生成があり、
これがデーモンと第2法則を整合させる』という主張をした。
しかしこれは特殊な測定モデルに基づいた主張であった.
一般には,エントロピー生成がゼロの(すなわち,熱力学的に可逆な)測定をすることは可能である。
そこでベネットが、ランダウア原理に基づき『情報の消去は論理的に不可逆なので、
熱力学的にも不可逆であり、それがデーモンと第2法則を整合させる』と主張した。
しかし第5 節でみたように、この主張は誤りである。実際には、(対称メモリの場合であっても)
情報消去は熱力学的に可逆にできる。したがって、1980 年代から広く受け入れられてきた
『情報の消去を考えることで初めて、デーモンと第2法則の整合性を理解できる』
という主張は妥当ではない。デーモンと第2法則の整合性を理解するために情報消去を考える必要は、
そもそもないのだ。第 6 節で議論したように
相互情報量をきちんと考慮に入れれば、
測定とフィードバックのプロセスそれぞれで、デーモンと第2法則が整合している
ことは明らかである。」
(沙川貴大、「情報処理の熱力学」、物性研究 電子版 4, 041209(2015), p.13)
この主張だけでも驚くが、最近、さらに驚くべき実験結果が報告された。高水 [3]によれば、2019年にG.B.レソビクらは量子コンピューター実験により、無秩序から秩序へと変化する現象を観測したとのことである [3,pp.123-128;22]。つまり、エントロピー増大の法則が破れていることが実験的に証明されたのかもしれない。これが本当であれば「逆転につぐ逆転」である。
重要な点が伝わっていないといけないので、要点だけもう一度述べておこう。ここまでの議論は、時間の向きがホンモノかニセモノかという議論である。「ホンモノ」の意味は、時間の向きが、我々という存在に関係ない客観的な性質(自然の本質)であるという意味だ。そして、ニセモノというのは、時間の向きが我々という認識者がいてはじめて成り立つ概念(主観的なもの)で、自然の本質ではない(幻に過ぎない)という意味である。
シラード、ブリルアン、ランダウア、沙川らは皆、エントロピー増大の法則を破ることはできないと言っている。つまり時間の向きはホンモノだということだ。それに対し、レソビクはエントロピーが減少しうると言っている。つまり、時間の向きはニセモノだということだろう。
時間に向き(非対称性)があるというのは単なる幻なのか。それとも自然の本質なのか。どちらだろう。現在、これらの分野は「情報熱力学」と呼ばれて急速に発展している。この分野がさらに進めば、マクスウェルの悪魔の問題も決着するかもしれない。今後の展開が楽しみな分野である。
・そもそもエントロピーは客観的な量か
「マクスウェルの悪魔」の話に戻ろう。「マクスウェルの悪魔」に関する研究の第二の流れは、エントロピー増大の法則が破れないこと(マクスウェルの悪魔が不可能なこと)を示す研究である。マクスウェルの死後、その流れがどうなっていったのかを紹介したい。
時間の非対称性に関するボルツマンの議論とマクスウェルの悪魔に関する議論を別々の流れとして説明したが、どちらの議論でも鍵となるのは「確率」である。ボルツマンはエントロピー増大の法則を気体分子運動論によって説明したが、そこで本質的な役割を果たしたのが確率だった。ニュートン力学は時間対称だが、確率は時間に非対称だ。だから、エントロピー増大を導出できる。
また、マクスウェルの悪魔についても確かに悪魔は物理的な仕事をしないが、悪魔は確率の法則を制御していた。それは情報の記録や消去、あるいは相互情報量に関係した過程を含むため、たとえマクスウェルの悪魔がいたとしてもエントロピー増大を免れないというのが、シラードに続く研究者たちの話の骨子だった。このように時間非対称性の起源の説明において「確率」は本質的な役割を果たしている。ところが、
「確率」が何かについては、科学でも哲学でもいまだに議論が続いており、はっきりしていない。
特に重要な問題は、確率が客観的な量か主観的な量かという問題だ。この点は今でも研究者の間で意見が分かれている。確率を客観的な量だと見なす立場(客観解釈)では、確率は仮想的な実験結果の「相対的な頻度」を表すと考えることが多い。例えば、「コイン投げで表が出る確率が2分の1である」とは、十分多い回数(例えば2億回)コインを投げれば、表が出る回数(相対頻度)はだいたい2分の1(つまりほぼ1億回)になるという意味である。
これに対し、主観的な量だと考える立場(主観解釈)では、確率とは私たちの「信念の度合い」を表していると考える。コイン投げの場合、「コイン投げで表が出る確率が2分の1である」とは、コインの構造に表と裏の差がなく、均等だから、出る確率も均等(つまり2分の1)だと信じられるという意味である。これら2つの考え方の重要な違いは、客観解釈が確率を自然の側(コインや台など)が持つ性質だと考えるのに対して、主観解釈は確率を我々の側の条件(知識の量など)によって決まる性質だと考える点である。これら2つの考え方は今も論争が続いている。
エントロピーは確率をもとに定義される。したがって、もし確率が主観的な量だということになれば、エントロピーもまた主観的な量ということになる。しかし、科学は客観性を重視し、そこで扱われる量はすべて(測定値や理論値など)客観的な量である。だから、もしエントロピーが主観的な量だということになれば、エントロピーは科学の対象から外れてしまう可能性がある。
物理学の世界には、エントロピーを主観的な量だと見る研究者と客観的な量だとする研究者が両方いる。
主観派は、私たちの識別能力に限界があるため、エントロピーが有限な値を持つだけで、エントロピーの本当の値はつねに0だと主張する。例えば、マクスウェルの悪魔のように識別能力に限界のない存在がいれば、すべては予測可能であり、確率は常に1になる。そのとき、エントロピーはつねに0である。
20世紀の著名な研究者であるW.パウリはエントロピーを主観的な量だと考えた。パウリ(1954)は次のように述べている[23,p.26]。「…一般的な自然法則によって許される最大限の知識量を我々が持つ場合、エントロピーは常にゼロである。」この考え方は確率の無知解釈に基づいていると思われる。知識の欠落が確率を生み出し、エントロピーをゼロでない値にしていると考えている。
これに対し、客観派は、私たちの能力に関係なく自然の本質としてランダムネスや確率が存在し、そのため(私たちの存在とは関係なく)エントロピーが有限な値を持つと考える。エントロピー増大の法則は真の物理法則というわけだ。エントロピーは客観的な量であると考える物理学者にP.W.アトキンスやI.プリコジンがいる。プリコジン(1995)は「不可逆性を、われわれが完全な知識を得た時には消えてしまう単なる見せかけのものと見なすわけにはいかない」と述べている[25,p.197]。また、アトキンス(1984) は、エントロピーが「無知の程度」として解釈されてしまう危険性があるとして、あえて「無秩序」や「秩序を破壊された」などの表現を使っている[26,p.195]。また、A.ベン‐ナイム(2010) は注意深く次のように表現している[26]。
「『エントロピーは知らないもの(未知)の度合いを測っている』と彼(ゲルマン)は注意深く言っている。
・・・『我々自身の無知』とは言っていない。・・・情報理論の中で情報は主観的量ではない。
・・・このように知らないもの(未知)は系に属する客観的な量であり、・・・『我々自身の無知』とは同じでない。」
(A.Ben-Naim(中嶋一雄訳),「エントロピーがわかる」,講談社(2010) p.194-195)
これらの言葉からわかるように、エントロピーの概念は物理学者たちの間でも意見が分かれている。
エントロピーと確率の客観性
なぜこんなに詳しくエントロピーの概念について解説し、その客観性にこだわっているのかというと、今後の議論がエントロピーの客観性に基礎を置いているからである。もしエントロピーが主観的な量だということになれば、本書の議論の土台は崩れる。だから、エントロピーが客観的な量だと見なせることを(少なくともそういう見方をする物理学者もたくさんいることを)述べておきたいのだ。
ここで、エントロピーに対する私の考えを明確にしておこう。私はエントロピーも確率も客観的な量として定義できると考えている。すべての確率が客観的だと言っているのではない。客観的に定義できる確率もあるということだ。確率は、我々の無知に起因した「主観確率」ばかりではない。観測者が存在しなくとも、自然現象は存在するし、その中に確率的な現象も存在する。
自然は、我々の無知に起因しない本質的なランダムネス(偶然)を含んでいる。例えばそれは量子力学的なランダムネスであるし、カオスに起因するものもある。いずれにせよ、自然は(無知と関係ない)本質的な偶然性を含む。だから、客観的な確率を定義できると考えられる。
カルロ・ロヴェッリは最近の著書「時間は存在しない」でこれに近い考え方を示している。彼はエントロピーの客観性について次のように説明している
「エントロピーはわたしたちが何を識別しないかによって変わってくる。なぜならそれは、わたしたちには区別できない配置の数で決まるからだ。まったく同じミクロな配置のエントロピーが、あるレベルのぼやけでは高くなり、別のレベルのぼやけでは低くなる。
だからといって、このぼやけは人間の精神が生み出したものではなく、あくまで実際に存在する物理的な相互作用によって決まる。エントロピーは恣意的でもなければ主観的な量でもなく、速度のような相対的な量なのだ。」
(C.Rovelli(富永星訳),「時間は存在しない」,NHK出版(2019) p.144)
ここに出てくる「ぼやけ」とは「粗視化」のことであり、簡単に言えば「見方の粗さ」のことである。ロヴェッリは、エントロピーが主観的な量ではなく、相対的な量であり、客観的な量だと言っている。その値は見方によって変わるが、それは主観的という意味ではない。
エントロピーは宇宙の中に実在する客観的な量であり、実際に宇宙の進化と共に増大している。エントロピー増大の法則は(私たちの無知に起因する見かけの法則ではなく)真の物理法則である。これが本書で私が採る立場である。
========================
【コラム】ボルツマンからアインシュタインへ(1):実証主義との対決
19世紀終わりにボルツマンとマッハの間で分子の実在性に関する論争があった。ボルツマンは多くの物理学者から批判を浴びたが、最後まで分子の実在性を信じていた。そして、「私は…これらの理論のために全力を挙げて戦う人間で唯一残っている者と言っていいかもしれない」とつぶやいた。まるでその論争を引き継ぐかのように、20世紀前半に量子力学が現れたとき、アインシュタインとボーアの間でも実在性に関する論争があった。アインシュタインは実証主義的な考え方に異論を唱え、「君は本当に自分が月を見ているときだけ、月が存在すると信じるのかい?」と不満を漏らした。ボルツマンとアインシュタインの状況は似ている。どちらも我々の観測から独立して世界が実在することを信じ、それゆえに追いつめられていった。筆者はボルツマンやアインシュタインの考え方に共感を覚える。やはりこの世界は、我々の観測から独立して存在するのではないだろうか。ただ、その現れ方(見え方)が観測のしかたに依存するだけである。
========================